机器学习-白板推导 11. 高斯混合模型
机器学习-白板推导 11. 高斯混合模型
1. GMM 介绍
通过将更基本的概率分布(如高斯分布)进行线性组合的叠加方法,可以被形式化为概率模型,被称为混合模型(mixture distributions)。
——PRML p82
而GMM(Gaussian Mxture Model)是将多个高斯分布线性叠加在一起的概率模型。
如下图所示一维高斯混合分布例子。(PRML p82)
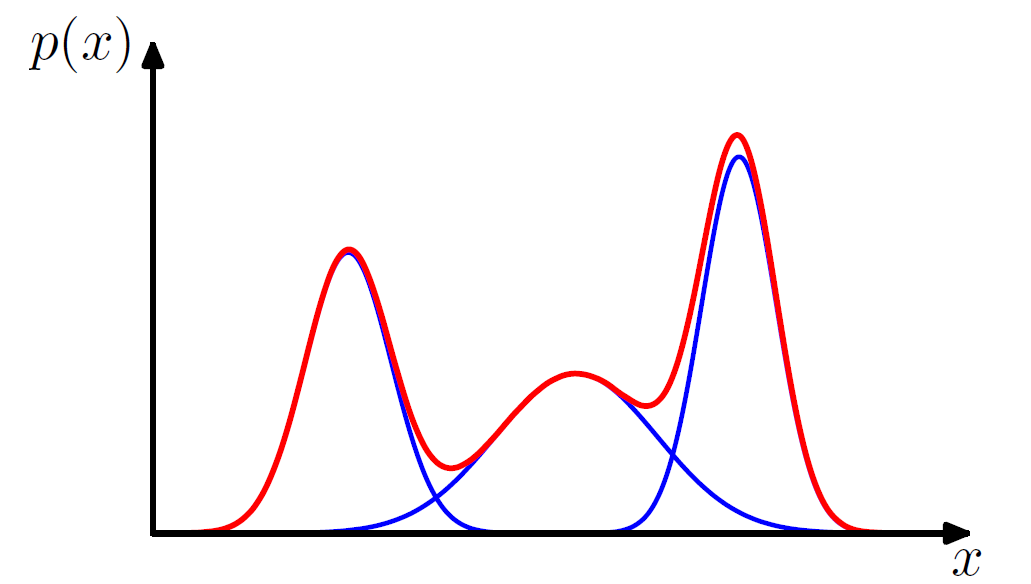
从两个角度来看GMM:
- 从几何角度:加权平均。
每个高斯分布可表示为,根据定义加权平均即:
- 从混合模型(或者生成模型)角度
我们假定数据为, 隐变量为,其中是属于哪个高斯分布的隐变量(离散随机变量)。
| z | … | |||
|---|---|---|---|---|
| p(z) | … |
这里相当于几何角度的加权权重。而根据上述定义画出高斯混合模型的概率图如下:

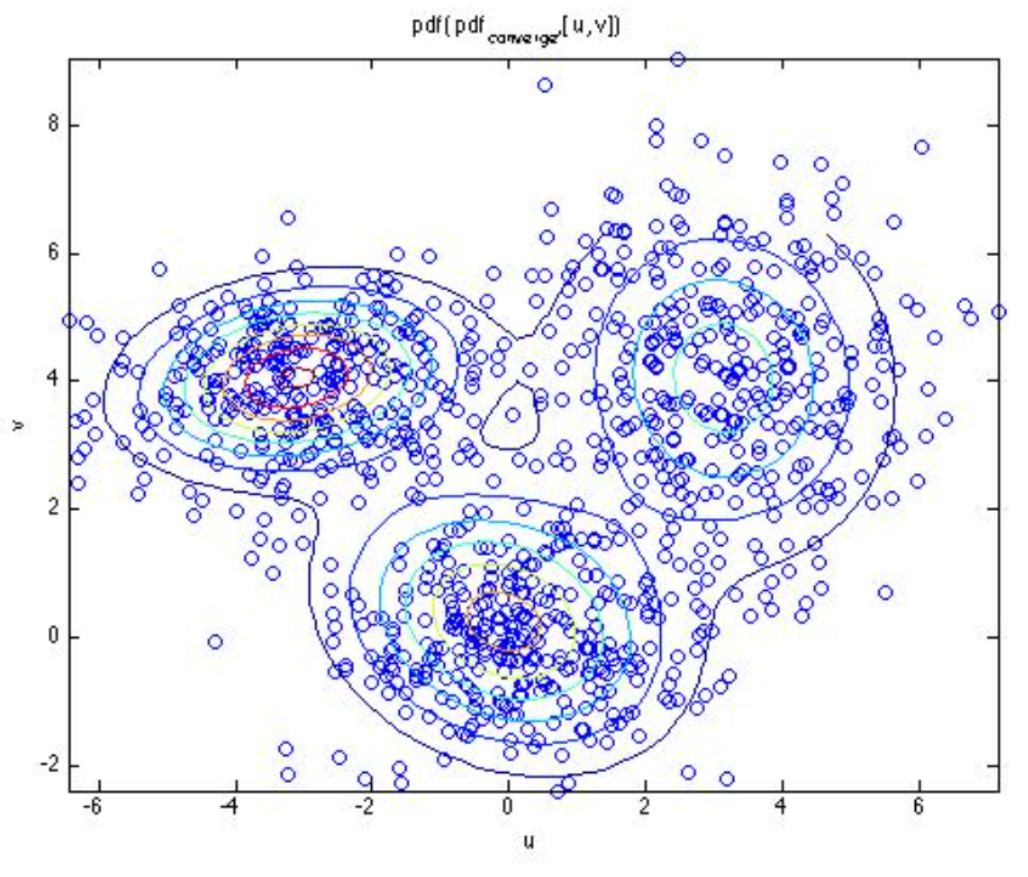
其中代表样本个数。实际上,如下图所示(徐亦达em讲义 ),对于每个样本点,有可能来自于这3个类别的高斯分布,只是概率大小不同而已,如上表所示对应不同的概率。这就是引入隐变量z的意义,它代表着我们无法确定的量,但是决定了样本的来自与来哪些高斯分布,我们计算时按照概率线性叠加来确定模型。
2. MLE来求解GMM
由上小节中,我们知道GMM的pdf由观测数据和隐变量来决定:
其中,现在,整个模型中数据和参数可表示为:
那么根据式2用MLE有:
对于式4,里面是连加,非常难以计算其解析解。一般使用EM算法来计算。
3. EM求解GMM(E步)
直接用EM 算法公式7结论,即Q函数:
我们发现要用到后验概率和联合概率。
根据式5有:
对于式7中,我们提出项来化简:
同理,我们可以得到简化表示,
综上,式7化简并用式6代入:
这里,由于是计算得到,跟无关,我们目的是求,不妨简写下。
根据式10, 11继续简化:
4. EM求解GMM(M步)
EM算法中M步的迭代公式为:
我们只介绍怎么求参数中的,其余参数类似求解,根据式12有:
这里将无关项忽略掉了,再利用拉格朗日乘子法有(转换为求极小值,加个负号):
式15对求偏导有:
因为对于所有的都要满足,那么有:
而,因此式17有:
再代入是式16中有:
这就是EM算法求解GMM模型参数的全部过程。


